تُعَدُّ المعادلات الرياضية جميلة إلى جانب أنها مفيدة. إضافة إلى أن العديد من العلماء يعترفون أنهم مغرمون بالعديد من المعادلات ليس فقط لأهميتهم ولكن لطريقة صياغتهم البسيطة التي تحمل في الوقت نفسه عمقًا وقدرة حقيقية على التعبير عن الواقع. فى هذا المقال سنعرض بعض المعادلات التي غيرت تاريخ العالم مع نبذة عن كل معادلة.
القانون الثاني للديناميكا الحرارية:

هو ما يصف خاصيات وسلوك انتقال الحرارة وإنتاج الشغل، سواء كان شغلا ديناميكيا حركيا، أم شغلا كهربائيا من خلال عمليات ثرموديناميكية.
ومنذ وضعت هذه القوانين أصبحت قوانين معتمدة ضمن قوانين الفيزياء والعلوم الفيزيائية (كيمياء، علم المواد، علم الفلك، علم الكون).
الأهمية:
يتناول القانون العلاقة بين الشغل والحرارة، ويعتبر القانون أساس عمل المحركات البخارية التي صاحبت الثورة الصناعية الكبرى في أوروبا، كما استخدم القانون في إثبات تكون المادة من ذرات عبر استخدام العلاقة بين الشغل والحرارة.
اللوغاريتمات

هي موضوع أساس في علم الرياضيات كما أنها أساسية في عمل وتنظيم برامج الحاسوب، وفي الكثير من القوانين العلمية الهامة، مثل: حساب أعمار الصخور، وعمر الكون، وأعمار اللوحات والآثار القديمة، ودرجة الحموضة وغيرها.
دخل مفهوم اللوجاريتمات إلى الرياضيات في أوائل القرن السابع عشر، على يد العالم “جون نابير” كوسيلة لتبسيط الحسابات.
الأهمية:
تكمن أهمية اللوجاريتمات في كونها طريقة ثورية لضرب الأرقام مرات متعددة في معادلة واحدة، لذلك صنعت نقلة نوعية في علم الفلك وتسيير المركبات، ورغم كون أهميتها تراجعت بعد ذلك بسبب ظهور وسائل تقنية أكثر دقة.
معادلة بلاك-شول

معادلة تفاضلية أخرى، تشرح بلاك-شول كيف يجد خبراء المال والتجار الأسعار للمشتقات. المشتقات (Derivatives) منتجاتٌ ماليةٌ ترتكز على بعض الأصول محل العقد [1] (underlying asset) مثل سهم، هي جزء جوهري من النظام المالي الحديث. تتيح معادلة بلاك-شول لمحترفي الأعمال المالية أن يحسبوا قيمة تلك المنتجات المالية، اعتمادًا على خصائص المشتق والأصول محل العقد.
نظرية الفوضى (Chaos Theory)

هذه المعادلة هي خريطة مايو/أيار اللوجستية. وهي تشرح عملية متطورة عبر الزمن:xt+1 x t 1 ، رتبة كمية ما x في دورة الزمن التالية. ومُعطاة في الصيغة التي في الصورة وتعتمد على xt وهو مستوى x في اللحظة الحالية. k هو ثابتٌ مختار. من أجل قيم مؤكدة من k، تبين الخريطة السلوك الفوضوي أنه إذا بدأنا عند قيمة ابتدائية محددة ما لـ x، ستتطور العملية بطريقة واحدة، ولكن إذا بدأنا عند قيمة ابتدائية أخرى حتى إن كانت قريبة جدًا جدًا للقيمة الأولى، ستتطور العملية بطريقة مختلفة كليًا. نرى السلوك الفوضوي -أي السلوك الحساس للظروف الابتدائية- في العديد من المجالات. الطقس كمثال كلاسيكي، فتغيّر صغير في الظروف الجوية في أحد الأيام قد يقود إلى أنظمة طقس مختلفة تمامًا في الأيام القليلة التالية، من الشائع تصورها بفكرة أن فراشة ترفرف أجنحتها على قارة متسببةً بإعصار على قارة أخرى.
قانون الجاذبية (Law of Gravity)

إن قانون نيوتن في الجذب يبين قوة الجاذبية بين جسمين F، ضمن حدود ثابت كوني G، كتلتا الجسمين m1 وm2 والمسافة بين الجسمين r. قانون نيوتن هو جزء بارز من التاريخ العلمي -فهو يفسر، بشكل تام تقريبًا، لماذا تتحرك الكواكب بالطريقة هذه، ومن الملحوظ أيضًا طبيعته الكونية- فهذه ليست فقط كيفية عمل الجاذبية على الأرض أو في نظامنا الشمسي، بل في أي مكان في الكون. صمدت جاذبية نيوتن بشكل جيد جدًا لمئتي عام، ولم تعد كذلك منذ نظرية أينشتاين في النسبية العامة التي قد تحل محلها.
معادلة هودجكن- هيكسلي

هي عبارة عن مجموعة معادلات تفاضلية لا خطية، التي تقرّب الخصائص الكهربائية للخلايا المُستثارة مثل العصبونات وخلايا القلب.
الأهمية:
تعد المعادلة طفرة في تأسيس علم البيولوجيا الرياضية، فقد استخدمت المعادلات الرياضية للمرة الأولى في نمذجة طريقة إرسال الإشارات العصبية.
وأصبحت المعادلة جزءًا رئيسيا من علم الأحياء في العامين الأخيرين، ويعتقد أنه سيكون لها استخدامات طبية موسعة خلال العقد المقبل. اقرأ أيضا:اخطر 10 فيروسات الكمبيوتر في العالم
معادلة شرودنجر من المعادلات الرياضية
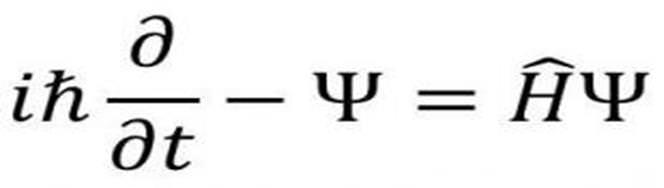
هي عبارة عن معادلة تفاضلية جزئية تصف كيفية تغير الحالة الكمية لنظام فيزيائي مع الزمن، وقد صاغها عالم الفيزياء النمساوي “إرفين شرودنجر” في أواخر عام 1925م، ونشرها عام 1926م.
تصف هذه المعادلة حالات النظم الكمومية المعتمدة على الزمن، وتحتل هذه المعادلة أهمية خاصة في ميكانيكا الكم، حيث تعد بمثابة قانون التحريك الثاني لنيوتن الذي يعتبر أساسيا في الفيزياء الكلاسيكية.
الأهمية:
تعد المعادلة أساس العديد من التطبيقات الالكترونية الحديثة، كالترانزستور وأشباه الموصلات، ويعزى لها الفضل في النقلات الكبيرة نحو استخدام الحاسب الآلي.
معادلة ماكسويل
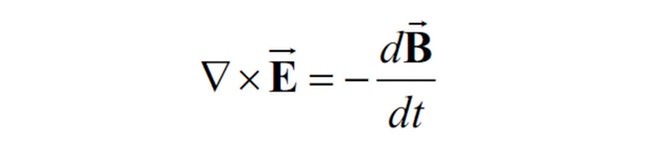
هي عبارة عن أربع معادلات تفاضلية جزئية، تصف سلوك وتغيرات المجالين الكهربائي والمغناطيسي، وتأثراتهما مع المادة، وتحولاتهما إلى أشكال أخرى من الطاقة.
وقد نشر الفيزيائي “جيمس كلارك ماكسويل” هذه المعادلات بين عامي 1861-1862م، وهذه المعادلات تصف العلاقات المتبادلة بين كل من المجالات الكهربائية والمجالات المغناطيسية والشحنات الكهربائية والتيار الكهربائي.
نص قانون ماكسويل في الكهرومغناطيسية: إذا انتقلت دائرة أو جزء من دائرة كهربائية مغلقة ضمن مجال مغناطيسي منتظم، فإنها تبذل شغلا يساوي شدة التيار الكهربائي المارة فيها في تغير التدفق المغناطيسي الذي يجتازها.
الأهمية:
تعد الكهرومغناطيسية أساس العديد من التقنيات الحديثة في مجال الاتصالات، كالرادار والتليفزيون وعمليات البث.
نظرية فيثاغورس من المعادلات الرياضية
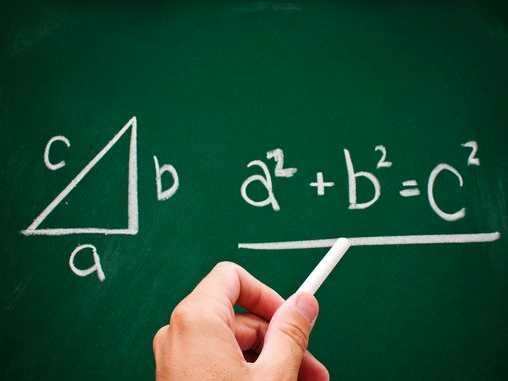
هي نظرية في الهندسة الإقليدية، تنص على أنه في أي مثلث قائم الزاوية يكون مجموع مربع طول الضلعين المحاذيين للزاوية القائمة مساويا لمربع طول الوتر.
سميت هذه المعادلة هكذا نسبة إلى العالم “فيثاغورس”، الذي كان رياضيا وفيلسوفا وعالم فلك في اليونان القديمة.
ونص المعادلة هو: في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة.
الأهمية:
تكمن أهمية المعادلة في أن أغلب تطبيقات الملاحة المستخدمة في عالمنا المعاصر ما زالت تستخدمها من أجل تحديد مواقع السفن والطائرات ومساراتها بدقة، كما تُعدُّ النظرية أحد أهم الأساسيات التي يعتمد عليها رسم الخرائط الجغرافية بشتى أنواعها .
النظرية الأساسية التفاضل والتكامل في المعادلات الرياضية

هي فرع من فروع الرياضيات والتي تطورت بشكل خاص على يد “إسحاق نيوتن”. وتدرس النهايات والاشتقاق والتكامل والمتسلسلات اللانهائية، وهو علم يستخدم لدراسة التغير في الدوال وتحليلها.
ويدخل علم التفاضل والتكامل في العديد من التطبيقات في الهندسة والعلوم المختلفة، حيث كثيراً ما يحتاج لدراسة سلوك الدالة والتغير فيها وحل المشاكل التي يعجز علم الجبر عن حلها بسهولة.
الأهمية:
تتعلق النظرية بشكل رئيسي بحسابات نهايات الدوال الرياضية، وتستخدم بشكل موسع في رسم المنحنيات الرياضية الخاصة بمختلف العلوم، كالإحصاء والاقتصاد وعلوم الحاسب بل والطب أحيانًا.
المراجع/https://www.businessinsider.com/17-equations-that-changed-the-world-2014-3?IR=T
